Em 1905, o médico russo (então estudante de pós-graduação) Nicolai Sergei Koroktoff propôs o método auscultatório para a medida indirecta da pressão arterial (esfigmomanometria).
Ouvir os sons de Koroktoff:
http://www.unb.br/fs/enf/nipe/korotkoffsom.html
A rede de canalização de uma casa envelhece. A nossa também!
(clique para ampliar)
Jean Louis Marie Poiseuille (1799 – 1896)
Definiu o fluxo, ou caudal, para um fluido viscoso e incompressível em escoamento laminar (desigando por fluido Newtoniano), como sendo:
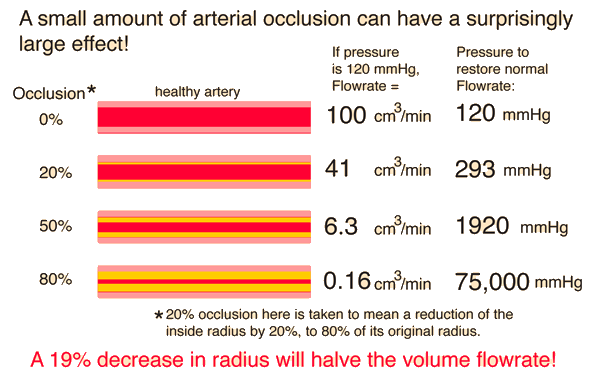
A unidade de viscosidade, µ ou η, é o Poise (simbolicamente, P)
Na referência: http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
[Ver: >Mechanics >Fluids >Poiseuille’s Law]
A pressão hidrostática varia com a profundidade. A pressão dinâmica varia com a velocidade.
Assim, se há movimento e desnível a pressão segue a equação de Bernoulli.
Na verdade, esta equação é deduzida com base em alguns pressupostos. Por exemplo, de que a energia se conserva. Ou seja, de que não actuam forças dissipativas. Isto é, a viscosidade é baixa e desprezável.
Portanto, a famosa equação de Bernoulli é válida, apenas, para o que se convenciona designar por “fluidos ideiais”.
Sr. Bernoulli, como voam as aves?
Daniel Bernoulli (1700–1782)
“Apercebendo-se do seu pombo correio a sobrevoar os telhados, Daniel Bernoulli parou a observá-lo. Quão maravilhoso era decerto voar… ”
“How a wing generates lift involves a combination of Bernoulli’s Principle AND Newton’s Third Law. Think of them working together on a wing to produce lift”.
http://downloads.cas.psu.edu/4h/AerospaceSupp/Activities/Flight/Overview/FlyLesson3.htm
http://piojo69.tripod.com/vuelo.htm
Nota 1: – Os Primeiros Vôos –
“In 1783, the first passengers in the colorful balloon were a sheep, rooster and duck. It climbed to a height of about 6,000 feet and traveled more than 1 mile.
After this first success, the brothers began to send men up in balloons. The first manned flight was on November 21, 1783, the passengers were Jean-Francois Pilatre de Rozier and Francois Laurent”.
(Referência: http://www.ueet.nasa.gov/StudentSite/historyofflight.html )
Nota 2: Este primeiro “voar” com balões (quase contemporâneo de Bernoulli) , tem mais a ver com o Princípio de Arquimedes (Impulsão) do que com o Princípio de Bernoulli.
Nota 3: O Primeiro Voar, ou Flutuar, em 1709!!
“No dia 8 de Agosto de 1709 [o jesuíta Bartolomeu de] Gusmão fez elevar a uns 4 metros de altura um pequeno balão de papel pardo grosso, cheio de ar quente, produzido pelo […] fogo material contido numa tigela de barro incrustada na base de um tabuleiro de madeira encerada…. As experiências sucederam-se com balões de muito maior envergadura e, finalmente, embora não haja provas irrefutáveis sobre o facto, consta que um balão, enorme, provavelmente voado pelo próprio Gusmão, foi lançado na praça de armas do castelo de S. Jorge e depois de percorrer 1 km veio a cair no Terreiro do Paço”.
(Referência: – Museu do Ar – http://www.emfa.pt/www/po/musar/historia/gusmao.php?lang=pt )
Não ficaria mal à Agência NASA (ver acima) fazer uma referência a esta experiência. Ainda que tratando-se de um vôo não tripulado.)
Daniel Bernoulli (1700 – 1782)
Médico de formação. Matemático por vocação.
Professor de Matemática na Academia Imperial de Ciências em Sampetersburgo, por convite de Catarina I, imperatriz da Rússia.
Um dos interesses de Bernoulli era saber como medir a pressão num fluido em movimento. O seu interesse centrava-se no que ocorria no fluxo sanguíneo. Ele intuía que pressão e velocidade estariam de algum modo relacionadas.
Qualititativamente, a sua equação foi então escrita como uma lei de conservação adaptada para fluidos:
pressão + vis viva = constante
A pressão e a vis viva representam, na mecânica dos sólidos, a altura e a energia cinética, respectivamente. Nos fluidos a massa é “trocada” pela densidade, ró.
p + ρ v2 = constante
Mais tarde, um século depois, o médico alemão Gustav G. Coriolis introduz na equação um factor de correcção, 1/2.
E a equação de Bernoulli, tal como hoje é conhecida é:
p + ρ g h + 1/2 ρ v2 = constante
